BARISAN DAN DERET

A. NOTASI SIGMA

Notasi sigma atau Σ digunakan untuk menyatakan operasi penjumlahan bilangan berurutan.

Sifat-sifat notasi sigma:

B. PENGERTIAN BARISAN DAN DERET

a. Pengertian Barisan

Barisan adalah rangkaian bilangan yang disusun menurut aturan atau pola tertentu.

Bentuk umum barisan adalah sebagai berikut:

U₁ , U₂, U₃, …. U_n

Keterangan:

U₁ = suku pertama

U₂ = suku kedua

U_n = suku ke-n

b. Pengertian Deret

Deret adalah penjumlahan suku-suku suatu barisan bilangan.

Bentuk umum deret adalah:

S_n = U₁ + U₂+ U_{3 +} …. + U_n

Keterangan:

S_n = jumlah n suku pertama

C. BARISAN DAN DERET ARITMETIKA

a. Barisan Aritmetika

Barisan aritmetika adalah barisan bilangan yang mempunyai beda (selisih) yang tetap/sama untuk setiap duku suku yang berurutan.

Bentuk umum barisan aritmetika adalah:

U₁, U₂, U₃, …. , U_n

a, a + b, a + 2b, …. , a + (n – 1)b

Pada barisan aritmetika terdapat beberapa rumusan sebagai berikut:

Rumus beda (b)

b = U_n – U_{n – 1}

b = U₂ – U₁ = U₃ – U₂

Rumus mencari suku ke-n

U_n = a + (n – 1)b

Keterangan:

U₁ = a = suku pertama/suku awal

U₂ = a + b

U₃ = a + 2b

U₄ = a + 3b

Contoh:

Barisan aritmetika:

5, 8, 11, 14, 17, ….

Tentukan suku ke-16?

Pembahasan:

b = U₂ – U₁ = 8 – 5 = 3

U_n = a + (n – 1)b

Suku ke – 16 adalah

U₁₆ = 5 + (16 – 1).3

= 5 + 45 = 50

b. Deret Aritmetika

Bentuk umum deret aritmetika adalah:

U₁+ U₂+ U₃+ …. + U_n

a + a + b + a + 2b + …. + a + (n – 1)b

Pada deret aritmetika terdapat rumusan sebagai berikut:

Rumus mencari jumlah n suku pertama

Keterangan: S_n = jumlah n suku pertama

Rumus mencari suku tengah

Jika banyak sukunya ganjil maka terdapat suku tengah (U_t):

Hubungan antara jumlah n suku pertama dan suku tengah adalah:

S_n = n x U_t

Contoh:

Deret aritmetika:

4 + 10 + 16 + 22 + 28 + ….

Tentukan jumlah 20 suku pertama!

Pembahasan:

D. BARISAN DAN DERET GEOMETRI

a. Barisan Geometri

Bentuk umum barisan geometri adalah sebagai berikut:

Pada barisan geometri terdapat beberapa rumusan sebagai berikut:

Rumus rasio (r)

Rumus mencari suku ke-n

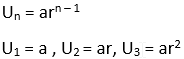
Contoh:

Diketahui barisan geometri:

1, 3, 9, 27, ….

Tentukan rasionya dan suku ke-7 (U₇)?

Pembahasan:

b. Deret Geometri

Bentuk umum dari deret geometri sebagai berikut:

Rumus mencari jumlah n suku pertama pada deret geometri:

Contoh:

Deret geometri:

4 + 8 + 16 + 32 + …

Tentukan jumlah 9 suku pertama?

Pembahasan:

E. DERET GEOMETRI TAK HINGGA

Deret geometri tak hingga adalah deret geometri yang memiliki jumlah suku sampai tak terhingga.

Deret geometri tak hingga dibedakan menjadi:

a. Deret Geometri Divergen

Syarat deret geometri divergen: jika r < – 1 atau r > 1

Contoh:

4 + 8 + 16 + 32 + …

S_∞ = ∞

S_∞= jumlah suku tak hingga

b. Deret Geometri Konvergen

Syarat deret geometri konvergen: jika –1 < r < 1

Contoh:

Maka rumus jumla suku sampai tak terhingga (S_∞) adalah:

Untuk jumlah tak hingga suku-suku ganjil adalah:

Sedangkan, jumlah tak hingga suku-suku genap adalah:

SOAL & PEMBAHASAN

1. Soal Ujian Nasional 2017

Sebuah unsur radioaktif meluruh menjadi setengahnya dalam waktu 30 menit. Jika pada mulanya massa unsur tersebut 20 gram, massa unsur yang meluruh selama 2 jam adalah …

1,25 gram
2,50 gram
10,00 gram
17,50 gram
18,75 gram

Pembahasan:

Jadi:

Jawaban: A

2. Soal Ujian Nasional 2017

Suku kedua dan kelima suatu barisan geometri adalah 3 dan 81. Jumlah n suku pertama barisan tersebut adalah …

Pembahasan:

Diketahui:

U₂= 3; U₅ = 81

Maka, a = 1

Jadi:

Jawaban: D

3. Soal Ujian Nasional 2017

Seutas tali dipotong menjadi 7 bagian dengan masing-masing potongan membentuk deret aritmetika. Bila potongan tali terpendek adalah 6 cm dan yang terpanjang 384 cm, panjang tali semula adalah …

1.375 cm
1.365 cm
1.265 cm
1.245 cm
762 cm

Pembahasan:

Diketahui: n = 7; a = 6; U_n = 384

Jawaban: B

4. Soal Ujian Nasional 2016

Suatu barisan artimetika memiliki suku kedua adalah 8, suku keempat adalah 14, dan suku terakhir 23. Jumlah semua suku barisan tersebut adalah ….

Pembahasan:

Diketahui: U₂ = 8; U₄ = 14

Substitusikan b = 3 maka:

a + b = 8

a = 8 – b = 8 – 3 = 5

Kemudian:

Jadi:

Jawaban: C

5. Seorang pedagang pada bulan pertama menabung sebesar Rp20.000,00. Ternyata usahanya sukses sehingga tiap bulan ia menabung kali tabungan bulan sebelumnya. Besar uang yang ditabung pedagang tersebut pada bulan keempat adalah ….

Rp151.875,00
Rp160.000,00
Rp162.500,00
Rp180.000,00
Rp192.000,00

Pembahasan:

Diketahui:

Jawaban: C

6. Soal SBMPTN 2017

Hasil bagi suku pertama oleh suku ke-3 suatu barisan aritmetika adalah . Jika suku ke-5 barisan tersebut adalah 12 maka suku ke-7 adalah ….

Pembahasan:

Substitusikan persamaan (1) maka:

12 = 2b + 4b

12 = 6b

b = 2

Maka, a = 2(2) = 4

Jadi:

U₇= a + 6b = 4 + 6(2) = 4 + 12 = 16

Jawaban: C

7. Soal SBMPTN 2016

Bilangan log(ab⁴) , log(a³b⁷), dan log(a⁶b⁹) merupakan tiga suku pertama barisan aritmatika. Jika suku ke-11 barisan tersebut adalah log(a^p) maka p = ….

Pembahasan:

Untuk barisan aritmetika berlaku hubungan:

Jawaban: B

8. Misalnya semua suku dari deret geometri adalah positif dan diketahui perbandingan suku ke-6 dan suku ke-4 dari deret tersebut adalah 16. Jika kuadrat suku pertama sama dengan rasionya maka jumlah empat suku pertama deret geometri adalah …..

Pembahasan: