Matematika SMP Aljabar

ALJABAR

A. PENGERTIAN ALJABAR

Aljabar adalah bentuk persamaan yang terdiri atas variabel (peubah) dan konstanta yang dihubungkan dengan tanda opeasi hitung serta tidak menggunakan tanda sama dengan (=).
Contoh:

1. 2x² + 9
2. x(x – 3)
3. p³ + 3p² + 2p – 1

B. UNSUR -UNSUR ALJABAR

a. Variabel, Koefisien dan Konstanta

• Varabel aljabar adalah lambang atau gabungan lambang yang mewakili sembarang bilangan dalam himpunan semestanya.
• Koefisien adalah nilai yang mengiringi variabel
• Konstanta adalah lambang aljabar yang menunjuk anggota tertentu (berupa bilangan) dalam himpunan semestanya.

Contoh:

5x² + 7x + 4y – 3

Maka:

• Variabelnya adalah x dan y

• Koefisiennya adalah 5, 7, dan 4

• Konstantanya adalah –3

b. Suku Aljabar dan Suku Sejenis

• Suku aljabar adalah seperangkat lambang aljabar yang dapat berupa variabel atau konstanta dan ditulis tanpa tanda operasi tambah atau kurang.

Contoh: 2x, xy, 4y²

• Suku-suku sejenis adalah suku-suku aljabar yang variabelnya dilambangkan dengan huruf dan pangkat yang sama.

Contoh:

2x² + 3x² – 3x – (2y + 5x)

Suku sejenis dari bentuk-bentuk aljabar di atas adalah 3x dan 5x serta 2x² dan 3x²

C. OPERASI PADA BENTUK ALJABAR

a. Penjumlahan dan Pengurangan

Suku-suku yang dijumlahkan atau dikurangkan harus suku yang sejenis.

Rumus:

ax + bx = (a + b)x

ax — bx = (a — b)x

Contoh:

1. 2a + 7a =(2 + 7)a = 9a
2. 2x + y + 4x – 5y = 2x + 4x + y – 5y

                               = (2 + 4)x + (1 – 5)y

                               = 6x – 4y

3. 5x² + 7x – 3x + 2x² = 5x² + 2x² + 7x – 3x

                            = 7x² + 4x

b. Perkalian

Variabel-variabel yang sejenis jika saling dikalikan maka hasilnya adalah perkalian koefisien variabel tersebut dan pangkatnya adalah jumlah pangkat variabel tersebut.

Contoh:

• y² . y = y^{2 + 1} = y³
• 3b³ . 4b² = 12b³⁺² = 12b⁵

Variabel yang tidak sejenis jika dikalikan maka hasilnya adalah perkalian koefisien variabel tersebut.

Contoh:

b x d = bd

2b x 3d = 6bd

b² x 3d = 3b²d

Sifat distributif pada perkalian

a(b + c) = ab + ac

(a + b)(c + d) = a(c + d) + b(c + d)

                 =  ac + ad + bc + bd

Contoh:

4x(x – 3y) = 4x² – 12xy

(2x + 5y)(x – 2y) = 2x(x – 2y) + 5y(x – 2y)

    = 2x² – 4xy + 5xy – 10y²

c. Pembagian

• Pembagian x : y dapat dinyatakan dengan pecahan 
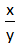
• Variabel-variabel yang tidak sejenis jika saling dibagi maka hasilnya adalah pembagian koefisien variabel tersebut.

Contoh:

• Variabel yangsejenis jika dibagi maka hasilnya akan seperti berikut:

d. Perpangkatan Bentuk Aljabar

Rumus:

p²         = p x p

p³         = p x p x p

(ab)²    = ab x ab = a²b²

Contoh:

(3b)²    = 3b x 3b = 9b²

(2a)³ = 2a x 2a x 2a = 8a³

–(3xy)³ = –{3xy . 3xy . 3xy}

      = –27x³y³

1. Perpangkatan bentuk aljabar suku dua

Rumus:

           (a + b)² = a² + 2ab + b²

                        (a – b)² = a² – 2ab + b²

                        (a + b)³ = a³ + 3a²b +3ab² + b³

                        (a – b)³ = a³ –  3a²b + 3ab² – b³

2. Segitiga Pascal

Digunakan untuk menentukan koefisien-koefisien hasil perpangkatan aljabar dua suku.

Contoh:

(a + b)³ = a³ + 3a²b + 3ab² + b³

→ koefisien 1, 3, 3, 1

(a + b)⁵ = a⁵ + 5a4b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

→ Koefisien 1, 5, 10, 10, 5, 1

Catatan: pada tiap suku, pangkat a semakin turun dan pangkat b semakin naik

D. MEMFAKTORKAN SUKU BENTUK ALJABAR

a. Bentuk Distributif

Memfaktorkan bentuk aljabar dapat digunakan rumus di bawah ini:

Rumus:

ax + ay = a(x + y)

ax – ay = a(x – y)

Catatan:

a dapat berupa koefisien atau variabel.

Contoh:

4x + 2xy = 2.2x + 1.2x.y

       = 2x (2 + 1y) = 2x(2 + y)

b. Faktorial Bentuk ax2 + bx + c dengan a = 1

Rumus:

x² + bx + c = (x + p)(x + q)

Syarat: b = p + q dan c = p.q

Contoh:

1. Tentukan faktor dari x² + 3x + 2!

x² + 3x + 2  = (x + p)(x + q)

p + q = 3; dan pq = 2

Maka, p = 2 dan q = 1

Jadi, x² + 3x + 2 = (x + 2)(x + 1)

c. Faktorisasi Bentuk ax2 + bx + c dengan a ≠ 1

Contoh:

Tentukan faktor dari 2x² + 3x + 1!

= 2x² + 3x + 1

= 2x² + 2x + x + 1

= (2x² + 2x) + (x + 1)

= 2x(x + 1) + (x + 1)

= (2x + 1)(x + 1)

d. Faktorisasi Selisih Dua Kuadrat (a2 – b2)

a² – b² = (a + b)(a – b)

Contoh:

1. x² – 49 = (x² – 7²) = (x + 7)(x – 7)

2. 9x² – 16y² = (3x)² – (4y)² = (3x + 4y)(3x – 4y)

e. FPB dan KPK Bentuk Aljabar

Untuk menentukan KPK dan FPB dari suatu bentuk aljabar digunakan cara sebagai berikut:

Contoh:

Tentukanlah KPK dan FPB dari 6x²y³ dan 15 x³y!

6x²y³ = 2.3.x².y³

15 x³y =  3.5.x³.y

→ KPK: ambil semua faktor dan jika ada yang sama ambil pangkat yang terbesar.

            Jadi, KPKnya adalah = 2.3.5.x³.y³ = 30 x³y³

→ FPB: pilih faktor yang sama dan terkecil pangkatnya.

            Jadi, FPBnya adalah = 3.x².y = 3x²y

E. PECAHAN BENTUK ALJABAR

a. Penjumlahan dan Pengurangan

Langkah-langkah untuk menyelesaikan penjumlahan atau pengurangan suatu pecahan bentuk aljabar adalah sebagai berikut:

• Menyamakan penyebut dari pecahan bentuk aljabar yang akan dijumlahkan atau dikurangkan.
• Jumlahkan atau kurangkan pembilang dari pecahan bentuk aljabar yang sudah disamakan penyebutnya.

Contoh:

b. Perkalian dan Pembagian

Rumus :

SOAL & PEMBAHASAN

1. Soal Ujian Nasional 2017

Bentuk sederhana dari 5×2 – 2xy – 8y2 – 6×2 – xy + 3y2 adalah ….

1. –x² – 3xy + 5y²
2. –x² – 3xy – 5y²
3. x² + xy – 5y²
4. x² + xy + 5y²

Pembahasan:

5x² – 2xy – 8y² – 6x² – xy + 3y² =  5x²  – 6x² – 2xy – xy – 8y² + 3y²

= – x² – 3xy – 5y²

Jawaban: B

2. Jika k merupakan penyelesaian dari 5(7x – 4) = –3(–9x + 12) + 8, nilai k – 7 adalah ….

1. –8
2. –6
3. –5
4. –2

Pembahasan:

5(7x – 4) = –3( –9x + 12) + 8

⇔ 35x – 20     = 27x – 36 + 8

⇔ 35x – 27x   = –36 + 8 + 20

⇔              8x  = –8

⇔                x  = = 1

Maka, x = k = 1

Jadi, k – 7 = 1 – 7 = –6

Jawaban: B

3. Soal Ujian Nasional 2015

Banyak kelereng Rian x buah, sedangkan kelereng Andri 3 buah kurangnya dari kelereng Rian. Jika jumlah kelereng mereka 18 buah, model matematika yang tepat adalah ….

1. A.2x + 3 = 18
2. 2x – 3 = 18
3. x + 3 = 18
4. x – 3 = 18

Pembahasan:

Misalkan: kelereng Rian → x

kelerang Andri →  x – 3

Rian + Andri = 18 → x + (x – 3) = 18

→ 2x – 3 = 18

Jawaban: B

4. Perhatikan pernyataan berikut!

1. 4x² – 9 = (2x + 3)(2x – 3)
2. 2x² + x – 3 = (2x – 3)(x + 1)
3. x² + x – 6 = (x + 3)(x – 2)
4. x² + 4x – 5 = (x – 5)(x + 1)

Pernyataan yang benar adalah …

1. I dan II
2. II dan III
3. I dan III
4. II dan IV

Pembahasan:

I. 4x² – 9 = (2x)² – 3²

= (2x + 3)(2x – 3)     (pernyataan (I) benar)

II. 2x² + x – 3 = (2x + 3)(x – 1) (pernyataan (II) salah)

III. x² + x – 6 = (x + 3)(x – 2)   (pernyataan (III) benar)

IV. x² + 4x – 5 = (x + 5)(x – 1) (pernyataan (IV) salah

Jadi, pernyataan (I) dan (II) benar.

Jawaban: C

5. Soal Ujian Nasional 2014

Jika x adalah penyelesaian dari 5x – 8 = 3x + 12, nilai dari x + 3 adalah ….

1. 13
2. 8
3. 5
4. –2

Pembahasan:

Jadi, nilai x + 3 = 10 + 3 = 13

Jawaban: A

6. Perhatikan pemfaktoran berikut ini!

1. 9ab + 21ac = 3a(3b + 7c)
2. x² – 9 = (x – 3)(x – 3)
3. 3p² – p – 2 = (3p + 2)(p –1)

Pemfaktoran tersebut yang benar adalah ….

1. (i) dan (ii)
2. (i) dan (iii)
3. (ii) dan (iii)
4. (i), (ii), dan (iii)

Pembahasan:

1. 9ab + 21ac = 3a(3b + 7c) (pernyataan (i) benar)
2. x² – 9 = (x – 3)(x + 3) (pernyataan (ii) salah)
3. 3p² – p – 2 = (3p + 2)(p – 1) (pernyataan (iii) benar)

Jadi, pernyataan (i) dan (iii) benar.

Jawaban: B

7. Soal UN 2013

Hasil dari (x – 2y)² adalah ….

1. x² + 4xy + 4y²
2. –x² – 4xy – 4y²
3. x² – 4xy + 4y²
4. x² + 4xy – 4y²

Pembahasan:

(x – 2y)² = (x – 2y)(x – 2y) = x² – 2xy – 2xy + 4y² = x² – 4xy + 4y²

Jawaban: C

8. Diketahui A = x – y dan B = 3x – 4y. Hasil dari A – B adalah ….

1. –2x + 3y
2. –2x – 5y
3. 2x – 5y
4. 2x – 3y

Pembahasan:

A – B =  (x – y) – (3x – 4y ) = x – y – 3x + 4y = x – 3x – y + 4y = –2x + 3y

Jawaban: A

9. Hasil dari 4p3q2 × 6p2r3 adalah ….

1. 10 p⁵ q² r³
2. 24 p⁵ q² r³
3. 24 p⁶ q² r
4. 24 p⁶ q² r³

Pembahasan:

4p³q² × 6p²r³ = (4 × 6) p^{3 + 2} q² r³ = 24 p⁵  q² r³

Jawaban: B

10. Bentuk sederhana dari adalah ….

Pembahasan

Jawaban: C