SEGITIGA
A. PENGERTIAN
Segitiga adalah suatu bangun datar yang dibatasi oleh tiga ruas garis dan memiliki tiga titik sudut.
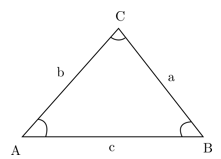
Keterangan:
AB, BC, AC disebut ruas garis
∠CAB = ∠A, ∠ABC = ∠B, ∠BCA = ∠C disebut titik sudut
Jumlah sudut segitiga adalah 180o
∠A + ∠B + ∠C = 180oP
B. JENIS-JENIS SEGITIGA
a. Jenis Segitiga Ditinjau dari sisi-sisinya
1. Segitiga sama kaki

2. Segitiga sama sisi-sisinya

3. Segitiga sembarang

b. Jenis Segitiga Ditinjau dari Sudut-sudutnya
1. Segitiga lancip
Segitiga lancip adalah segitiga yang ketiga sudutnya berupa sudut lancip (kurang dari 90o).
2. Segitiga tumpul
Segitga tumpul adalah segitiga yang salah satu sudutnya tumpul (lebih dari 90o)
3. Segitiga siku-siku
Segitiga siku-siku adaalah segitiga yang salah satu sudutnya siku-siku (90o)
C. KELILING DAN LUAS SEGITIGA
a. Rumus Keliling Segitiga
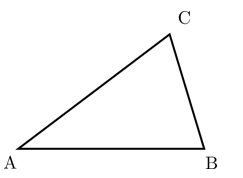
Keliling = Jumlah panjang sisi-sisinya = AB + BC + CA
b. Rumus Luas Segitiga
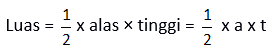

D. DUA SEGITIGA KONGRUEN (SAMA DAN SEBANGUN)
Dua buah bangun dikatakan kongruen jika:
- Sisi-sisi yang bersesuaian sama panjang (sisi, sisi, sisi)
- Sudut-sudut yang bersesuaian sama besar
Syarat-syarat dua segitiga kongruen jika:
- Ketiga sisi yang bersesuaian sama panjang (sisi, sisi, sisi)

- Dua sisi yang sama panjang dan satu sudut sama besar (sisi, sudut, sisi)
- Satu sisi sama panjang dan dua sudut sama besar (sudut, sisi, sudut)
E. SEGITIGA YANG SEBANGUN
Dua buah segitiga dikatakan sebangun apabila:

- Sudut-sudut yang seletak sama besar
- Sisi-sisi yang bersesuaian sebanding

Maka:
∠A = ∠P , ∠B = ∠Q , ∠C = ∠R
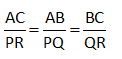

F. SUDUT DALAM DAN SUDUT LUAR

Keterangan:
∠A1 , ∠B1 , ∠C1 , adalah sudut dalam
∠A2 , ∠B2 , ∠C2 , adalah sudut luar
Besarnya sudut luar pada suatu titik sudut sama dengan jumlah dua sudut dalam pada dua titik sudut lainnya.
Rumus:
∠A2 = ∠B1 + ∠C1
∠B2 = ∠A1 + ∠C1
∠C2 = ∠A1 + ∠B1
G. TEOREMA PYTHAGORAS
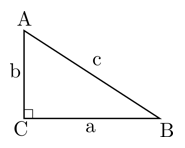
Sisi AB disebut dengan hipotenusa (sisi miring)
Rumus:
c2 = a2 + b2
Tripel Pythagoras: 3 bilangan bulat yang membentuk segitiga siku-siku.
Tabel tripel Pythagoras:
| a | b | c |
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 7 | 24 | 25 |
| 8 | 15 | 17 |
| 9 | 40 | 41 |
SOAL & PEMBAHASAN
1. Soal Ujian Nasional 2017
Diketahui segitiga KLM dan segitiga PQR kongruen. Besar ∠KLM = 740, ∠KML = 460, ∠PQR = 600, dan ∠PRQ = 460. Pasangan sisi yang sama panjang pada kedua segitiga itu adalah ….
- KM = PR
- LM = QR
- KL = PQ
- KM = PQ
Pembahasan:
Pembahasan:
| ∆ KLM | ∆PQR |
| ∠KML = 460 → ∠M ∠KLM = 740 → ∠L ∠LKM = 60o → ∠K | ∠PRQ = 460 → ∠R ∠QPR = 740 → ∠P ∠PQR = 600 → ∠Q |
Maka diperoleh pasangan sisi yang sama panjang adalah:
ML = RP; LK = PQ; dan MK = RQ
Jawaban: C
2. Perhatikan gambar!
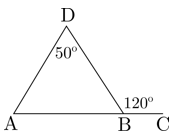
Besar ∠BAD adalah ….
- 50
- 60
- 70
- 80
Pembahasan:
∠BAD + ∠ADB = ∠CBD
∠BAD = ∠CBD – ∠ADB = 120o – 50o = 70 o
Jawaban: c
3. Soal Ujian Nasional 2016
Perhatikan gambar di bawah!

Luas daerah yang diarsir adalah ….
- 45
- 54
- 72
- 81
Pembahasan:

Jawaban: c
4. Sebuah kapal berlayar sejauh 100 km ke arah timur, kemudian berbelok ke arah utara sejauh 75 km. Jarak terpendek kapal tersebut dari titik awal adalah ….
- 175 km
- 125 km
- 100 km
- 75 km
Pembahasan:

Jarak terpendek adalah:
![]()
Jawaban: B
5. Andi ingin mengetahui lebar sungai. Di seberang sungai terdapat sebuah pohon. Untuk itu dia menancapkan tongkat pada posisi A, B, C, dan D dengan ukuran seperti pada gambar. Andi ingin mengukur lebar sungai dari tongkat D sampai pohon. Berapa lebar sungai tersebut?

- 11 m
- 12 m
- 15 m
- 16 m
Pembahasan:

Jawaban: B
6. Seorang anak mempunyai tinggi 150 cm dan panjang bayangannya 250 cm. Pada saat yang sama panjang bayangan sebatang pohon 15 m, tinggi pohon tersebut adalah ….?
- 9 m
- 10 m
- 12 m
- 25 m
Pembahasan:
Dengan menggunakan prinsip kesebangunan maka diperoleh persamaan:
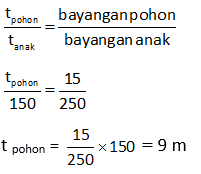
Jawaban: A
7. Sebuah tiang tingginya 12 m, berdiri tegak di atas tanah datar. Dari ujung atas tiang ditarik seutas tali ke sebuah patok pada tanah. Jika panjang tali 15 m, jarak patok dengan pangkal bagian bawah adalah ….?
- 13,5 m
- 10 m
- 9 m
- 3 m
Pembahasan:
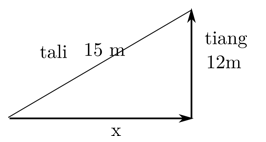
Karena merupakan segitiga siku-siku maka berlaku:
![]()
Jawaban: C
8. Soal Ujian Nasional 2014
Perhatikan gambar!

Diketahui:
AB = 12 cm
CD = 7 cm
AD = 8 cm
DE = 8 cm
Panjang CE adalah ….
- 10 cm
- 8 cm
- 7 cm
- 6 cm
Pembahasan:
Segitiga ABC sebangun dengan segitiga EDC sehingga diperoleh:
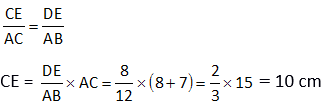
Jawaban: A







